Curriculum Vitae
I am a researcher in nonlinear dynamics and theoretical neuroscience, interested in how collective dynamics emerge in complex systems and in the transitions between physiological and pathological regimes, with the aim of understanding their underlying dynamical mechanisms.
I studied physics at the Free University of Berlin, where my academic interests coalesced around nonlinear dynamics and dynamical systems, leading to a thesis in mathematical cosmology. This focus carried over into my doctoral research at the Weierstrass Institute for Applied Analysis and Stochastics (WIAS), as a member of the Collaborative Research Center CRC 910 and formally enrolled as a PhD student at the Technical University of Berlin. During my time at WIAS, I studied mode-locking and synchronization phenomena in coupled nonlinear oscillator systems.
I am currently working at the RIKEN Center for Brain Science, where I develop and analyze biophysical models of neural and glial systems to study collective dynamics in physiological and pathological regimes. My research includes modeling epileptic dynamics, calcium signaling in astrocyte networks, and dynamical phenomena such as chaos in spatially extended oscillator systems.
📄 CV
Research
My research integrates nonlinear dynamical systems with theoretical neuroscience. This includes the study of collective dynamics in coupled oscillators and excitable systems, with emphasis on biophysical models of neurons and astrocytes. A central theme of my work is the characterization of dynamical patterns associated with neurological disorders, such as epilepsy. To this end, I develop and apply mean-field descriptions—especially within the Ott–Antonsen framework—and use bifurcation theory to investigate critical transitions to uncover structural relations between distinct regimes of neural activity.
Research Interests
Nonlinear dynamics of coupled oscillatory and excitable systems form the basis of my research, both as complex physical systems and as models of brain activity. Insights gained from studying dynamics informs the development and analysis of biophysical models, providing a theoretical framework for describing neurological disorders. Current areas of investigation include:
Coupled nonlinear systems
- Synchronization pattern and topologically protected incoherent states
- Properties of extensiv chaos
- Resource-controlled population activity
- Pattern formation in coupled excitable systems
- Active rotator with noise and adaptive-feedback
Brain dynamics
- Metabolic feedback mechanisms (including ketogenic interventions)
- Calcium dynamics in astrocyte networks (Li-Rinzel)
- Continuous and discrete attractor networks (MEC, CA3) and epilepsy
- Computational modeling of grid-cell activity
Publications
Control of seizure-like dynamics in neuronal populations with excitability adaptation related to ketogenic diet
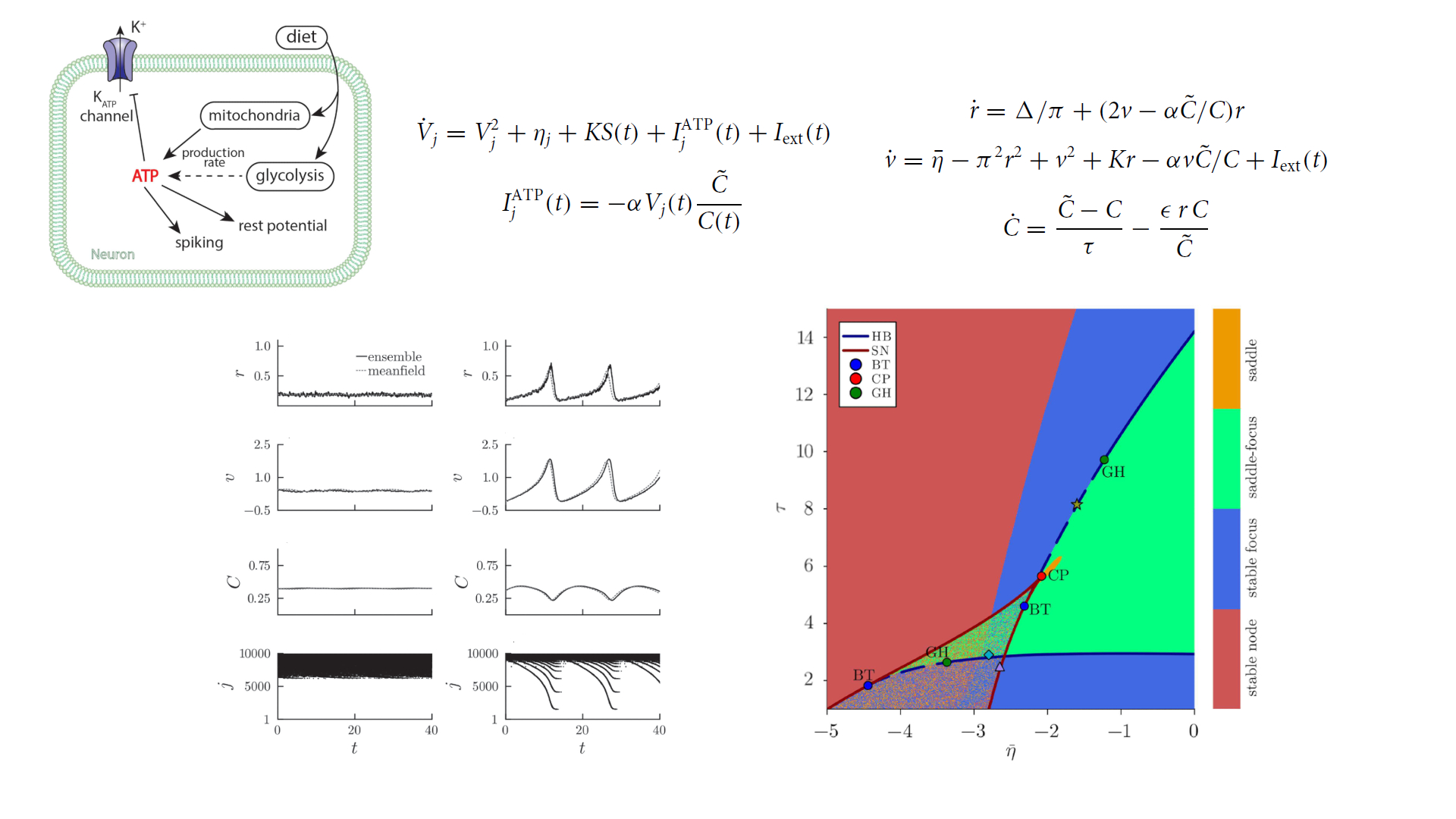
Abstract
We consider a heterogeneous, globally coupled population of excitatory quadratic integrate-and-fire neurons with excitability adaptation due to a metabolic feedback associated with ketogenic diet, a form of therapy for epilepsy. Bifurcation analysis of a three-dimensional mean-field system derived in the framework of next-generation neural mass models allows us to explain the scenarios and suggest control strategies for the transitions between the neurophysiologically desired asynchronous states and the synchronous, seizure-like states featuring collective oscillations. We reveal two qualitatively different scenarios for the onset of synchrony. For weaker couplings, a bistability region between the lower- and the higher-activity asynchronous states unfolds from the cusp point, and the collective oscillations emerge via a supercritical Hopf bifurcation. For stronger couplings, one finds seven co-dimension two bifurcation points, including pairs of Bogdanov–Takens and generalized Hopf points, such that both lower- and higher-activity asynchronous states undergo transitions to collective oscillations, with hysteresis and jump-like behavior observed in vicinity of subcritical Hopf bifurcations. We demonstrate three control mechanisms for switching between asynchronous and synchronous states, involving parametric perturbation of the adenosine triphosphate (ATP) production rate, external stimulation currents, or pulse-like ATP shocks, and indicate a potential therapeutic advantage of hysteretic scenarios.
Citation: Eydam, S., Franović, I., & Kang, L. (2024). Control of seizure-like dynamics in neuronal populations with excitability adaptation related to ketogenic diet. Chaos: An Interdisciplinary Journal of Nonlinear Science, 34(5), 053128. https://doi.org/10.1063/5.0180954
Collective Activity Bursting in a Population of Excitable Units Adaptively Coupled to a Pool of Resources
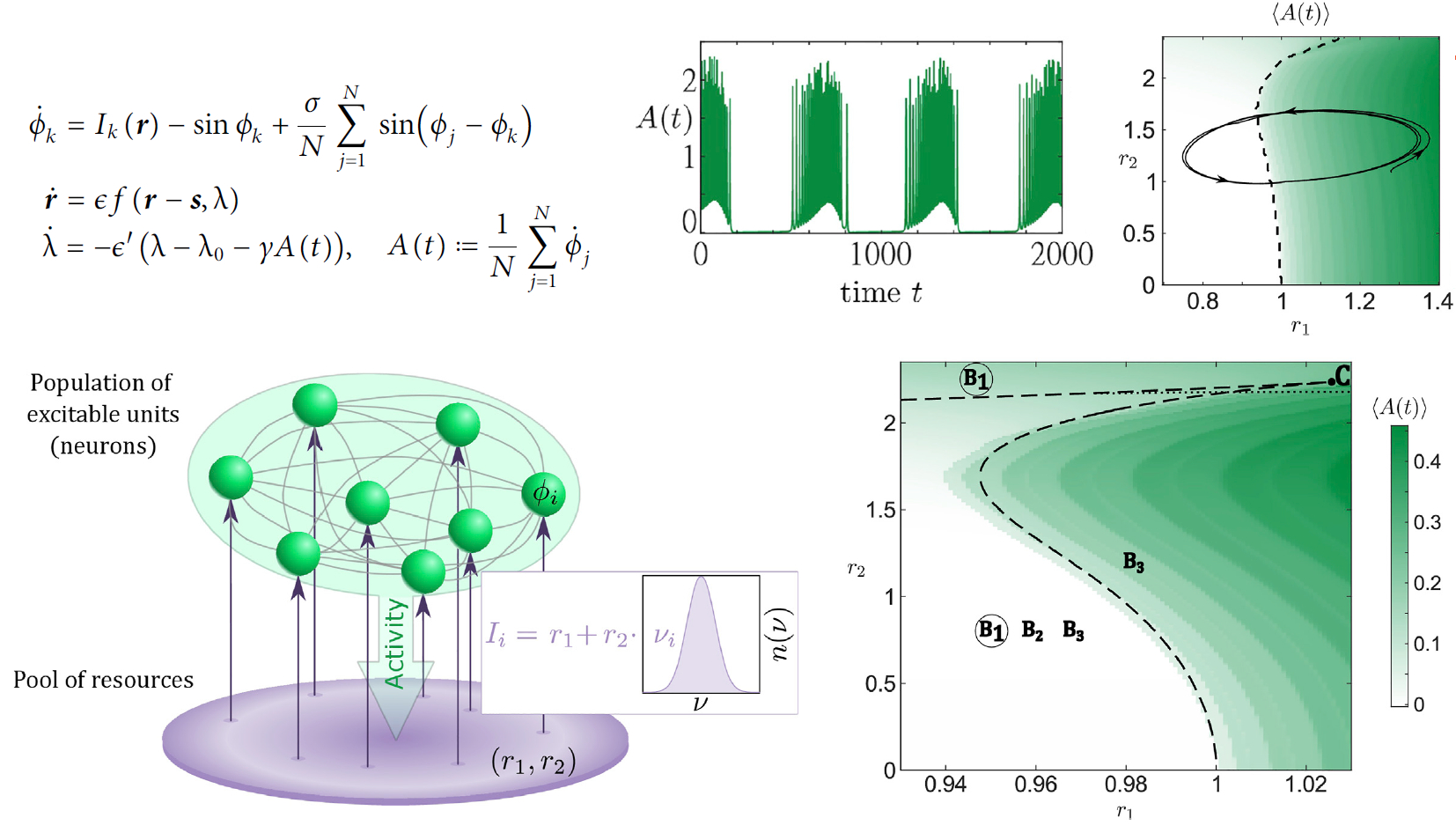
Abstract
We study the collective dynamics in a population of excitable units (neurons) adaptively interacting with a pool of resources. The resource pool is influenced by the average activity of the population, whereas the feedback from the resources to the population is comprised of components acting homogeneously or inhomogeneously on individual units of the population. Moreover, the resource pool dynamics is assumed to be slow and has an oscillatory degree of freedom. We show that the feedback loop between the population and the resources can give rise to collective activity bursting in the population. To explain the mechanisms behind this emergent phenomenon, we combine the Ott-Antonsen reduction for the collective dynamics of the population and singular perturbation theory to obtain a reduced system describing the interaction between the population mean field and the resources.
Citation: Franović, I., Eydam, S., Yanchuk, S., & Berner, R. (2022). Collective Activity Bursting in a Population of Excitable Units Adaptively Coupled to a Pool of Resources. Frontiers in Network Physiology, Volume 2 - 2022. https://doi.org/10.3389/fnetp.2022.841829
Dynamics of a stochastic excitable system with slowly adapting feedback
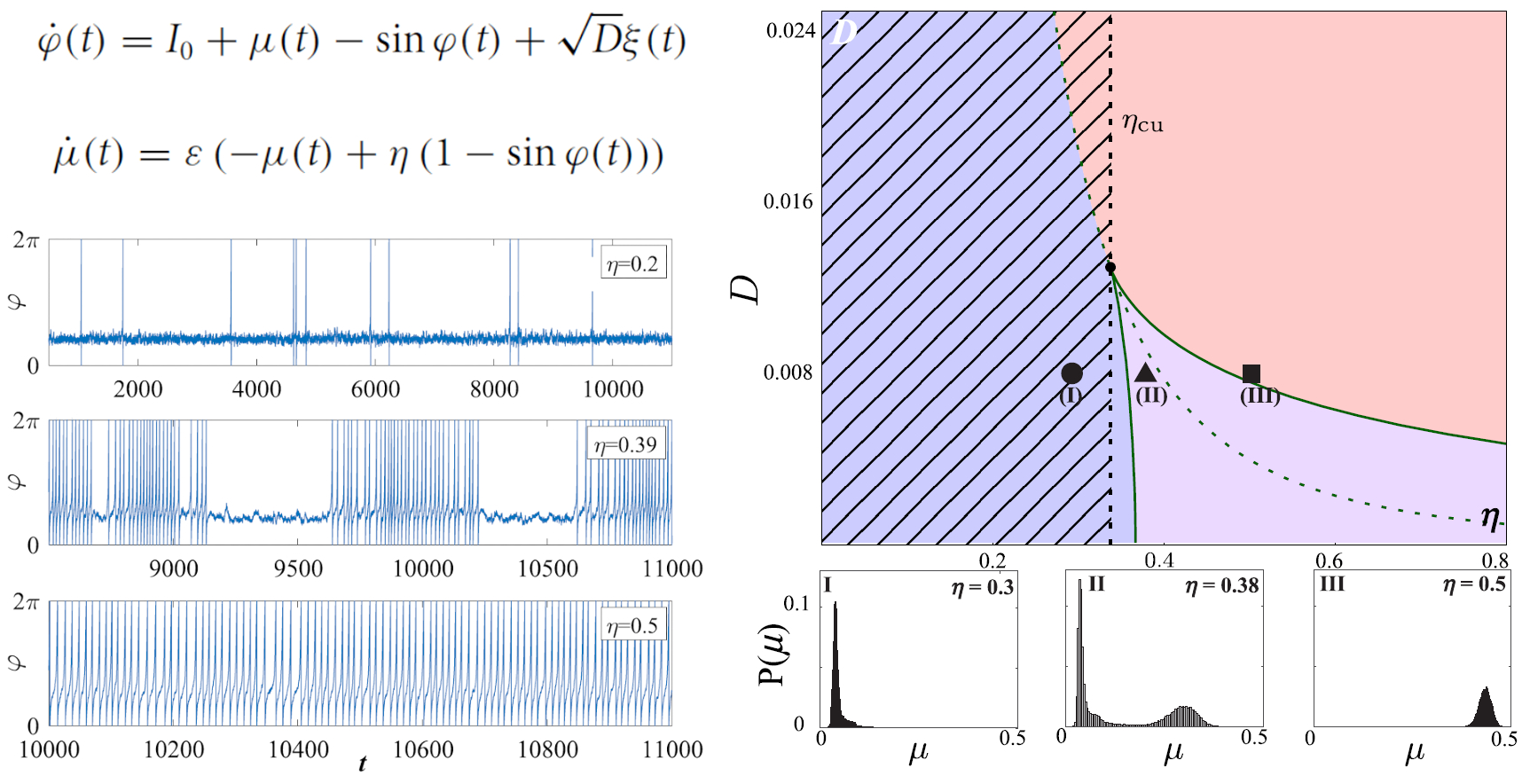
Abstract
We study an excitable active rotator with slowly adapting nonlinear feedback and noise. Depending on the adaptation and the noise level, this system may display noise-induced spiking, noise-perturbed oscillations, or stochastic bursting. We show how the system exhibits transitions between these dynamical regimes, as well as how one can enhance or suppress the coherence resonance or effectively control the features of the stochastic bursting. The setup can be considered a paradigmatic model for a neuron with a slow recovery variable or, more generally, as an excitable system under the influence of a nonlinear control mechanism. We employ a multiple timescale approach that combines the classical adiabatic elimination with averaging of rapid oscillations and stochastic averaging of noise-induced fluctuations by a corresponding stationary Fokker–Planck equation. This allows us to perform a numerical bifurcation analysis of a reduced slow system and to determine the parameter regions associated with different types of dynamics. In particular, we demonstrate the existence of a region of bistability, where the noise-induced switching between a stationary and an oscillatory regime gives rise to stochastic bursting.
Citation: Franović, I., Yanchuk, S., Eydam, S., Bačić, I., & Wolfrum, M. (2020). Dynamics of a stochastic excitable system with slowly adapting feedback. Chaos: An Interdisciplinary Journal of Nonlinear Science, 30(8), 083109. https://doi.org/10.1063/1.5145176
News
🎙️ Conference Presentation | July 6, 2026
Glutamate-Induced Calcium Signaling in Astrocyte Networks
FENS-Forum 2026, Barcelona
🌍 Conference Visit | March 12, 2026
COSYNE26
Lisbon — Looking forward to connecting!
